» Trottola d'inerzia secondo Maxwell (0660)

Immagini

DESCRIZIONE

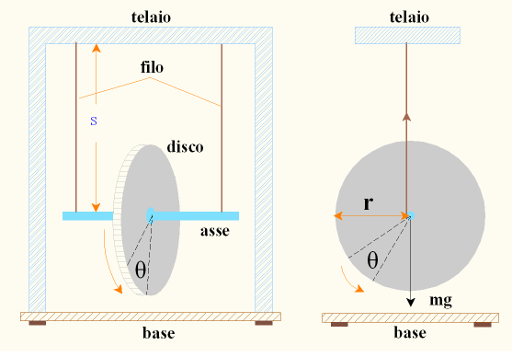
Su una base rettangolare di metallo con quattro piedini di gomma, è fissato un telaio metallico rettangolare cui è sospeso un piccolo disco d'acciaio. Il disco è sospeso mediante due fili, paralleli e di uguale lunghezza, attaccati alle estremità dell'asse del disco (una barretta di acciaio che passa per il centro del disco). I fili possono essere avvolti nello stesso verso sull'asse (Vedi Foto-1 e Disegno-1). Lasciando libero il disco ad una certa altezza, i fili si srotolano ed esso acquista energia cinetica, sia di traslazione verso il basso che di rotazione intorno all'asse. Appena i fili sono svolti completamente arrivando all'altezza minima, cominciano a riavvolgersi in senso opposto ed il disco sale verso l'alto, trasformando l'energia cinetica in energia potenziale. Alla posizione di massima altezza l'energia è tutta potenziale, mentre alla minima altezza l'energia potenziale è minima e quella cinetica è massima.

Questo dispositivo è praticamente uno yo-yo di grandi dimensioni e serve per dimostrare l'inerzia di moto ed il principio di conservazione dell'energia. Il disco, abbandonato dopo averlo fatto ruotare in modo da avvolgere i fili sul suo asse, discende con moto accelerato e risale per inerzia; il fenomeno si ripete più volte fino al completo arresto del disco per effetto degli attriti. La differenza con lo yo-yo consiste nel fatto che qui il disco è sorretto da due fili fissati al suo asse, mentre nello yo-yo un solo filo scorre entro la scanalatura presente lungo la circonferenza del disco. Nello yo-yo, inoltre, il moto di sali-scendi può essere mantenuto spingendo verso il basso il disco quando è nel punto più alto, fornendogli quindi ulteriore energia.

Se il disco cade dall'altezza S, la perdita di energia potenziale = m g S, dove m è la massa del disco (di raggio r) e dell'asse (di raggio trascurabile rispetto ad r). Questa energia è acquisita dal disco come energia cinetica di rotazione e di traslazione.

Se ω è la velocità angolare che il disco ha acquistato cadendo dalla distanza S, la sua energia cinetica di rotazione è $Formula: [ \frac{1}{2} I\omega^2]$ , dove I è il momento d'inerzia del disco attorno l'asse perpendicolare al suo piano; l'energia cinetica di traslazione è $Formula: [\frac{1}{2}mv^2 ]$ dove v è la velocità lineare finale.

Quindi

Equazione: [ mgS = \frac{1}{2} I\omega^2+\frac{1}{2}mv^2 ]

Siccome:

Equazione: [ \omega^2 = \frac{v^2}{r^2} ]

dove r è il raggio del disco.

Quindi

Equazione: [ mgS = \frac{1}{2} I\frac{v^2}{r^2} + \frac{1}{2}mv^2 ]

o anche

Equazione: [\frac{1}{2} I\frac{v^2}{r^2} = mg S - \frac{1}{2}mv^2]

La velocità media del disco $Formula: [ v_m = \frac{S}{t}]$ , dove t è il tempo di caduta del disco a distanza S, quindi la velocità del disco è $Formula: [ v = \frac{2S}{t}]$ , e $Formula: [ v^2 = \frac{4S^2}{t^2} ]$
Da questa relazione si può ricavare il momento d'inerzia del disco:

Equazione: [ I = mr^2\bigg(\frac{gt^2}{2S} -1\bigg )]

BIBLIOGRAFIA

[1] MATHUR, D. S. Elements of Properties of Matter. S. Chand CO., 1959.

Dati Catalografici

Data di costruzione:	---
Data di carico:	Ignota
Nr. Inventario:	Ignoto (Ignoto)
Costruttore:	Costruttore sconosciuto
Materiale:	acciaio, metallo, gomma
Dimensioni:	Base: 28 cm x 15 cm x 2,5 cm; Altezza totale: 37 cm; Diametro del disco: 10 cm; Lunghezza dei fili: 20 cm; lunghezza dell'asse: 4 cm
Conservazione:	buono

» Trottola d'inerzia secondo Maxwell (0660) Eng Ita

Immagini

DESCRIZIONE

BIBLIOGRAFIA

Dati Catalografici

» Trottola d'inerzia secondo Maxwell (0660)